12-02. 反応拡散モデル
02. ギーラー-マインハルト系の反応拡散モデルについてプログラムを組み,様々なパタンを描く¶
以下の方針で取り組んでみよう.
- モデルの離散化
- 2次元拡散方程式を参考にプログラムを組む
- 初期値の設定
- 拡散係数(Du, Dv)を変化させてどのようなパタンが生じるか調べる
プログラムの例¶
作成方針を以下に示す.
# 02-p. 2次元の反応拡散モデルの擬似コード
各種パラメータ,初期値の設定
場の設定(x,y)
結果を記録するリストの定義
uの初期化
vの初期化
for ステップ数 in 繰り返し回数:
時刻tの計算
# -- 状態遷移 --
情報の更新
結果のリストへの記録場の更新をおこなう関数updateを定義してみよう.
Solution to Exercise 1
def rd_u(u_arr, v, D_u, d_u, k_1, k_2, dh, dt):
new_u = (
u_arr[1, 1]
+ (
D_u
* (u_arr[0, 1] + u_arr[2, 1] + u_arr[1, 0] + u_arr[1, 2] - 4 * u_arr[1, 1])
/ (dh**2)
- d_u * u_arr[1, 1]
+ k_1 * u_arr[1, 1] ** 2 / v
+ k_2
)
* dt
)
return new_u
def rd_v(v_arr, u, D_v, d_v, k_3, dh, dt):
new_v = (
v_arr[1, 1]
+ (
D_v
* (v_arr[0, 1] + v_arr[2, 1] + v_arr[1, 0] + v_arr[1, 2] - 4 * v_arr[1, 1])
/ (dh**2)
- d_v * v_arr[1, 1]
+ k_3 * u**2
)
* dt
)
return new_v
def update(u, v, D_u, D_v, d_u, d_v, k_1, k_2, k_3, dh, dt):
"""反応拡散モデルに基づくuの更新
場の更新をおこなう.
周期境界条件を仮定している.
Args:
u,v: アクチベーターとインヒビターの現在の場の配列
D_u, D_v: 拡散係数
d_u, d_v: 分解率
k_1: アクチベーターの自己活性化・インヒビターによる抑制
k_2: アクチベーターの基本的な生成
k_3: アクチベーターによるインヒビターの生産促進
Returns:
u_new, v_new: 次世代の場の配列
"""
n_i, n_j = u.shape
new_u = np.zeros((n_i, n_j), dtype=u.dtype)
new_v = np.zeros((n_i, n_j), dtype=u.dtype)
for i in range(n_i):
for j in range(n_j):
if i == 0:
if j == 0:
# 境界条件処理 i=0,j=0
new_u[i, j] = rd_u(
u[[-1, 0, 1], :][:, [-1, 0, 1]],
v[i, j],
D_u,
d_u,
k_1,
k_2,
dh,
dt,
)
new_v[i, j] = rd_v(
v[[-1, 0, 1], :][:, [-1, 0, 1]], u[i, j], D_v, d_v, k_3, dh, dt
)
elif 0 < j < n_j - 1:
# 境界条件処理 i=0,0<j<n_j-1
new_u[i, j] = rd_u(
u[[-1, 0, 1], :][:, [j - 1, j, j + 1]],
v[i, j],
D_u,
d_u,
k_1,
k_2,
dh,
dt,
)
new_v[i, j] = rd_v(
v[[-1, 0, 1], :][:, [j - 1, j, j + 1]],
u[i, j],
D_v,
d_v,
k_3,
dh,
dt,
)
elif j == n_j - 1:
# 境界条件処理 i=0,j=n_j-1
new_u[i, j] = rd_u(
u[[-1, 0, 1], :][:, [n_j - 2, n_j - 1, 0]],
v[i, j],
D_u,
d_u,
k_1,
k_2,
dh,
dt,
)
new_v[i, j] = rd_v(
v[[-1, 0, 1], :][:, [n_j - 2, n_j - 1, 0]],
u[i, j],
D_v,
d_v,
k_3,
dh,
dt,
)
elif 0 < i < n_i - 1:
if j == 0:
# 境界条件処理 1<i<n_i-1,j=0
new_u[i, j] = rd_u(
u[[i - 1, i, i + 1], :][:, [-1, 0, 1]],
v[i, j],
D_u,
d_u,
k_1,
k_2,
dh,
dt,
)
new_v[i, j] = rd_v(
v[[i - 1, i, i + 1], :][:, [-1, 0, 1]],
u[i, j],
D_v,
d_v,
k_3,
dh,
dt,
)
elif 0 < j < n_j - 1:
# メイン (1<i<n_i-1,1<j<n_j-1)
new_u[i, j] = rd_u(
u[[i - 1, i, i + 1], :][:, [j - 1, j, j + 1]],
v[i, j],
D_u,
d_u,
k_1,
k_2,
dh,
dt,
)
new_v[i, j] = rd_v(
v[[i - 1, i, i + 1], :][:, [j - 1, j, j + 1]],
u[i, j],
D_v,
d_v,
k_3,
dh,
dt,
)
elif j == n_j - 1:
# 境界条件処理 1<i<n_i-1,j=n_j-1
new_u[i, j] = rd_u(
u[[i - 1, i, i + 1],][:, [n_j - 2, n_j - 1, 0]],
v[i, j],
D_u,
d_u,
k_1,
k_2,
dh,
dt,
)
new_v[i, j] = rd_v(
v[[i - 1, i, i + 1],][:, [n_j - 2, n_j - 1, 0]],
u[i, j],
D_v,
d_v,
k_3,
dh,
dt,
)
elif i == n_i - 1:
if j == 0:
# 境界条件処理 i=n_i,j=0
new_u[i, j] = rd_u(
u[[n_i - 2, n_i - 1, 0],][:, [-1, 0, 1]],
v[i, j],
D_u,
d_u,
k_1,
k_2,
dh,
dt,
)
new_v[i, j] = rd_v(
v[[n_i - 2, n_i - 1, 0],][:, [-1, 0, 1]],
u[i, j],
D_v,
d_v,
k_3,
dh,
dt,
)
elif 0 < j < n_j - 1:
# 境界条件処理 i=n_i-1,1<j<n_j-1
new_u[i, j] = rd_u(
u[[n_i - 2, n_i - 1, 0],][:, [j - 1, j, j + 1]],
v[i, j],
D_u,
d_u,
k_1,
k_2,
dh,
dt,
)
new_v[i, j] = rd_v(
v[[n_i - 2, n_i - 1, 0],][:, [j - 1, j, j + 1]],
u[i, j],
D_v,
d_v,
k_3,
dh,
dt,
)
elif j == n_j - 1:
# 境界条件処理 i=n_i-1,j=n_j-1
new_u[i, j] = rd_u(
u[[n_i - 2, n_i - 1, 0],][:, [n_j - 2, n_j - 1, 0]],
v[i, j],
D_u,
d_u,
k_1,
k_2,
dh,
dt,
)
new_v[i, j] = rd_v(
v[[n_i - 2, n_i - 1, 0],][:, [n_j - 2, n_j - 1, 0]],
u[i, j],
D_v,
d_v,
k_3,
dh,
dt,
)
return (new_u, new_v)update関数を使ってシミュレーションをしてみよう.
Solution to Exercise 2
import numpy as np
import matplotlib.pyplot as plt計算時間がそれなりにかかるので,場の範囲をともに(-20,20)とする.
以下の例では,計算時間は(環境によるが)だいたい3分程度はかかる.
D_u = 1.2 # 拡散係数 D_uを1~1.5ぐらいで動かす
D_v = 10 # 拡散係数
d_u = 1.0
d_v = 1.0
k_1 = 1.0
k_2 = 0.05
k_3 = 1.0
dt = 0.02 # 時間方向の刻み幅
dh = 1 # 空間方向の刻み幅
x = np.arange(-20, 20, dh)
y = np.arange(-20, 20, dh)
xmesh, ymesh = np.meshgrid(x, y)
T = 300
nEnd = int(T / dt) # 時間に関するループの繰り返し数
print("繰り返し数: ", nEnd)
t_list = [] # 時刻を記録するリスト
u_list = [] # uを記録するリスト
v_list = [] # vを記録するリスト
# u,vの初期化
u = np.ones([len(x), len(y)], dtype=float)
u = u + np.random.uniform(0, 0.01, size=u.shape)
v = np.ones([len(x), len(y)], dtype=float)
v = v + np.random.uniform(0, 0.01, size=u.shape)
t_list.append(0)
u_list.append(np.copy(u))
v_list.append(np.copy(v))
for n in range(nEnd):
t = n * dt # 時刻tの計算
# -- 状態遷移 --
u_tmp, v_tmp = update(u, v, D_u, D_v, d_u, d_v, k_1, k_2, k_3, dh, dt)
# 情報の更新
u = np.copy(u_tmp)
v = np.copy(v_tmp)
if n % 5000 == 0:
print("Steps: ", n)
if n % 50 == 0:
t_list.append(t)
u_list.append(np.copy(u))
v_list.append(np.copy(v))
print(len(t_list))繰り返し数: 15000
Steps: 0
Steps: 5000
Steps: 10000
301
最終状態をプロットしてみる.
i = -1
fig, ax = plt.subplots(1, 2, figsize=(16, 8))
ax[0].set_aspect("equal")
pcm = ax[0].pcolormesh(xmesh, ymesh, u_list[i], alpha=0.75)
fig.colorbar(pcm, ax=ax[0], shrink=0.75)
ax[1].set_aspect("equal")
pcm = ax[1].pcolormesh(xmesh, ymesh, v_list[i], alpha=0.75)
fig.colorbar(pcm, ax=ax[1], shrink=0.75)
title = [
"D_u = " + str(D_u),
"D_v = " + str(D_v),
"d_u = " + str(d_u),
"d_v = " + str(d_v),
"k_1 = " + str(k_1),
"k_2 = " + str(k_2),
"k_3 = " + str(k_3),
]
fig.tight_layout()
fig.suptitle(", ".join(title) + "; t=" + str(t_list[i]), fontsize=20)
plt.show()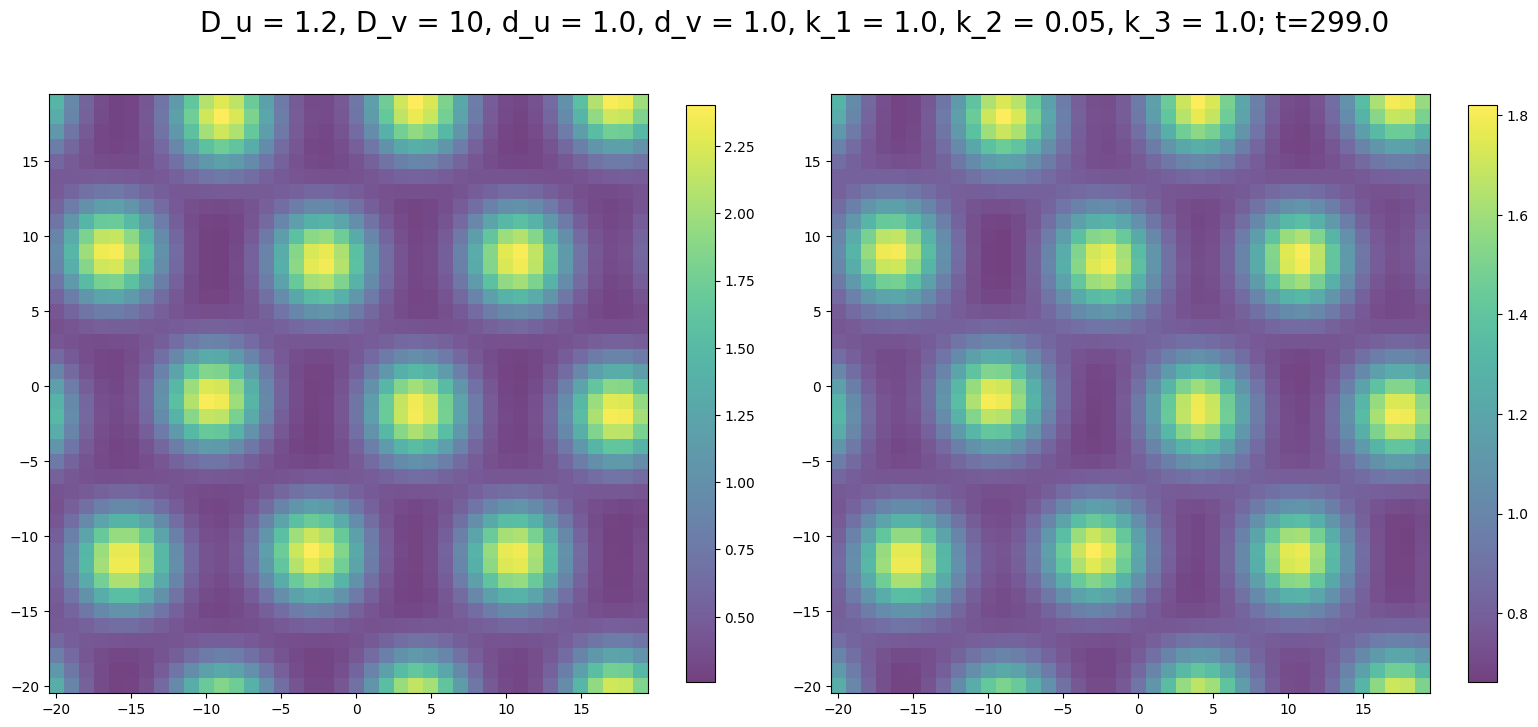
時間発展もプロットしてみよう.
step = 15
fig, axes = plt.subplots(4, 5, figsize=(20, 16))
for i in [i * step for i in range(20)]:
ax = axes.flat[i // step]
ax.set_aspect("equal")
pcm = ax.pcolormesh(xmesh, ymesh, u_list[i], alpha=0.75, cmap="gray")
fig.colorbar(pcm, ax=ax, shrink=0.75)
ax.set_title("t = " + str(t_list[i]))
title = [
"D_u = " + str(D_u),
"D_v = " + str(D_v),
"d_u = " + str(d_u),
"d_v = " + str(d_v),
"k_1 = " + str(k_1),
"k_2 = " + str(k_2),
"k_3 = " + str(k_3),
]
fig.tight_layout()
fig.suptitle(", ".join(title))
plt.show()
おまけ:リファクタリング¶
先のupdate関数ではforループを使っているため処理に時間がかかる.
NumPyの配列とベクトル化された計算を活用することで高速化できる.
高速化すると,計算で考慮する場の範囲や時間をより広く,長く取ることが可能になる.
Solution to Exercise 3
def laplacian(f, dh):
"""ラプラシアン
周期境界条件を仮定している.
Args:
f: 関数(スカラー場)の配列
dh: 空間解像度(1セルの幅)
Returns:
f_laplacian: fのラプラシアンの配列
"""
f_ext = np.zeros((f.shape[0] + 2, f.shape[1] + 2), dtype=f.dtype)
f_ext[1:-1, 1:-1] = f[:, :]
f_ext[0, 1:-1] = f[-1, :]
f_ext[-1, 1:-1] = f[0, :]
f_ext[1:-1, 0] = f[:, -1]
f_ext[1:-1, -1] = f[:, 0]
f_c = f_ext[1:-1, 1:-1]
f_n = f_ext[0:-2, 1:-1]
f_e = f_ext[1:-1, 2:]
f_s = f_ext[2:, 1:-1]
f_w = f_ext[1:-1, 0:-2]
f_laplacian = (f_n + f_e + f_s + f_w - 4 * f_c) / dh**2
return f_laplacian
def update_v2(u, v, D_u, D_v, d_u, d_v, k_1, k_2, k_3, dh, dt):
"""反応拡散モデルに基づくuの更新
場の更新をおこなう.
周期境界条件を仮定している.
Args:
u,v: アクチベーターとインヒビターの現在の場の配列
D_u, D_v: 拡散係数
d_u, d_v: 分解率
k_1: アクチベーターの自己活性化・インヒビターによる抑制
k_2: アクチベーターの基本的な生成
k_3: アクチベーターによるインヒビターの生産促進
Returns:
u_new, v_new: 次世代の場の配列
"""
u_new = u + (D_u * laplacian(u, dh) - d_u * u + k_1 * u**2 / v + k_2) * dt
v_new = v + (D_v * laplacian(v, dh) - d_v * v + k_3 * u**2) * dt
return (u_new, v_new)改善されたupdate_v2関数をもちいてシミュレーションしてみよう.
先ほどと同様の(ただし範囲を広く,時間を長くとった)シミュレーションでも高速に処理できる.
D_u = 1.3 # 拡散係数 D_uを1~1.5ぐらいで動かす
D_v = 10 # 拡散係数
d_u = 1.0
d_v = 1.0
k_1 = 1.0
k_2 = 0.05
k_3 = 1.0
dt = 0.02 # 時間方向の刻み幅
dh = 1.0 # 空間方向の刻み幅
x = np.arange(-50, 50, dh)
y = np.arange(-50, 50, dh)
xmesh, ymesh = np.meshgrid(x, y)
T = 3000
nEnd = int(T / dt) # 時間に関するループの繰り返し数
print("繰り返し数: ", nEnd)
t_list = [] # 時刻を記録するリスト
u_list = [] # uを記録するリスト
v_list = [] # vを記録するリスト
# u,vの初期化
u = np.ones([len(x), len(y)], dtype=float)
u = u + np.random.uniform(0, 0.01, size=u.shape)
v = np.ones([len(x), len(y)], dtype=float)
v = v + np.random.uniform(0, 0.01, size=u.shape)
t_list.append(0)
u_list.append(np.copy(u))
v_list.append(np.copy(v))
for n in range(nEnd):
t = n * dt # 時刻tの計算
# -- 状態遷移 --
u_tmp, v_tmp = update_v2(u, v, D_u, D_v, d_u, d_v, k_1, k_2, k_3, dh, dt)
# 情報の更新
u = np.copy(u_tmp)
v = np.copy(v_tmp)
if n % 10000 == 0:
print("Steps: ", n)
if n % 50 == 0:
t_list.append(t)
u_list.append(np.copy(u))
v_list.append(np.copy(v))
print(len(t_list))繰り返し数: 150000
Steps: 0
Steps: 10000
Steps: 20000
Steps: 30000
Steps: 40000
Steps: 50000
Steps: 60000
Steps: 70000
Steps: 80000
Steps: 90000
Steps: 100000
Steps: 110000
Steps: 120000
Steps: 130000
Steps: 140000
3001
i = -1
fig, ax = plt.subplots(1, 2, figsize=(16, 8))
ax[0].set_aspect("equal")
pcm = ax[0].pcolormesh(xmesh, ymesh, u_list[i], alpha=0.75)
fig.colorbar(pcm, ax=ax[0], shrink=0.75)
ax[1].set_aspect("equal")
pcm = ax[1].pcolormesh(xmesh, ymesh, v_list[i], alpha=0.75)
fig.colorbar(pcm, ax=ax[1], shrink=0.75)
title = [
"D_u = " + str(D_u),
"D_v = " + str(D_v),
"d_u = " + str(d_u),
"d_v = " + str(d_v),
"k_1 = " + str(k_1),
"k_2 = " + str(k_2),
"k_3 = " + str(k_3),
]
fig.tight_layout()
fig.suptitle(", ".join(title) + "; t=" + str(t_list[i]), fontsize=20)
plt.show()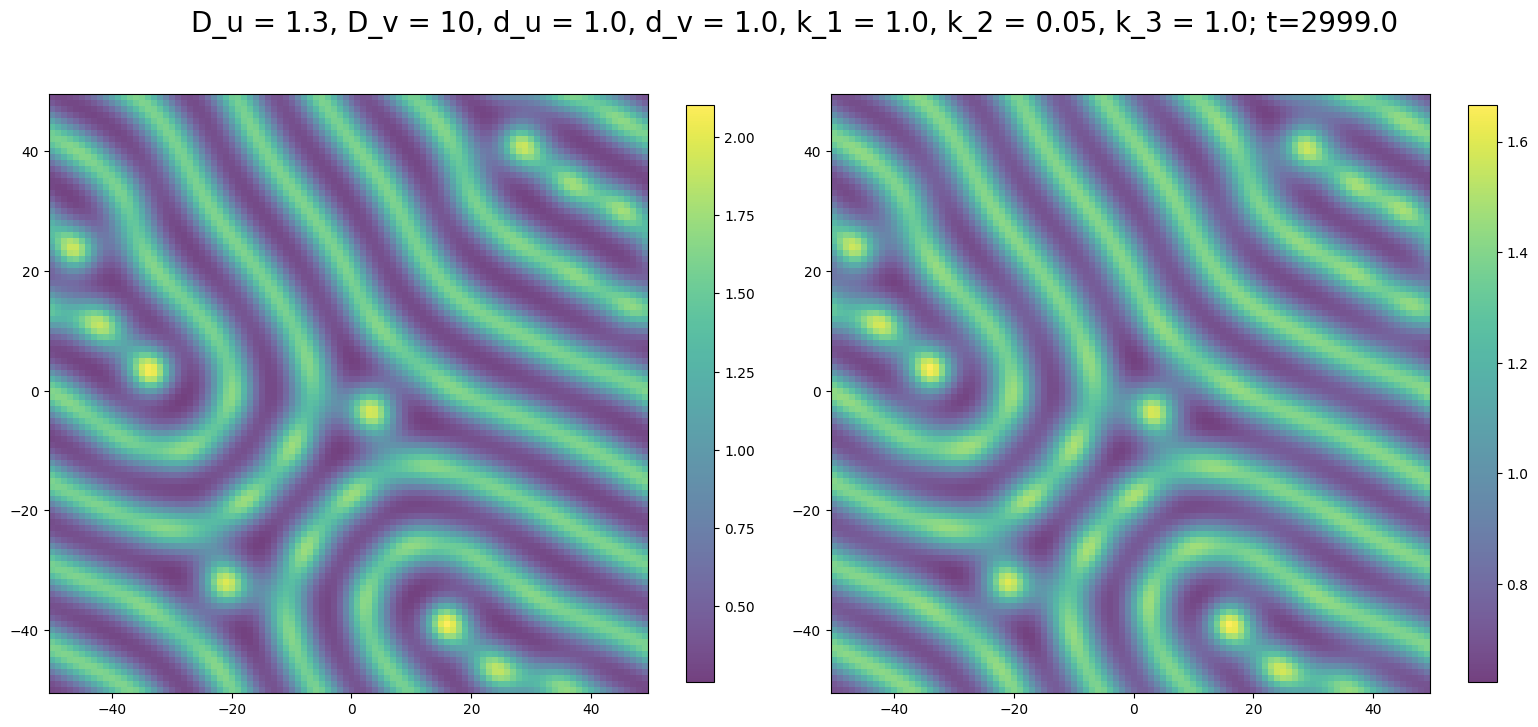
step = 150
fig, axes = plt.subplots(4, 5, figsize=(20, 16))
for i in [i * step for i in range(20)]:
ax = axes.flat[i // step]
ax.set_aspect("equal")
pcm = ax.pcolormesh(xmesh, ymesh, u_list[i], alpha=0.75, cmap="gray")
fig.colorbar(pcm, ax=ax, shrink=0.75)
ax.set_title("t = " + str(t_list[i]))
title = [
"D_u = " + str(D_u),
"D_v = " + str(D_v),
"d_u = " + str(d_u),
"d_v = " + str(d_v),
"k_1 = " + str(k_1),
"k_2 = " + str(k_2),
"k_3 = " + str(k_3),
]
fig.tight_layout()
fig.suptitle(", ".join(title))
plt.show()