12-01. 拡散方程式 - 数理生物学演習

01-01. １次元の拡散方程式¶

１次元の拡散方程式のプログラムを書く．固定境界条件（ $u(0,t) = u_0, u(x_e,t) = 0$ ）でシミュレーションしてみよう．

# 01-01-01. １次元の拡散方程式の関数定義
# 時間方向はオイラー法，空間方向は中心差分


def diff_eq_1d(u_arr, D, dh, dt):
    new_u = u_arr[1] + D * ((u_arr[0] + u_arr[2] - 2 * u_arr[1]) / (dh**2)) * dt
    return new_u

# 01-01-02. １次元拡散モデルのシミュレーション実行
import numpy as np

D = 1.0  # 拡散係数
dt = 0.05  # 時間方向の刻み幅
dx = 0.5  # 空間方向の刻み幅
u_0 = 1  # 境界条件 u(0,t) = u_0
x_e = 10  # xの終端
t_end = 50  # tの終端

x = np.arange(0, x_e, dx)  # x座標
t_list = []  # 時刻を記録するリスト
u_list = []  # uを記録するリスト

u = np.zeros(len(x), dtype=float)  # uの初期化
u[0] = u_0  # 境界条件 u(0,t) = u_0
u[-1] = 0  # 境界条件 u(x_e,t) = 0

t_list.append(0)
u_list.append(np.copy(u))

for n in range(1, int(t_end / dt) + 1):
    t = n * dt  # 時刻tの計算
    u_tmp = np.zeros(len(x), dtype=float)

    u_tmp[0] = u_0  # 境界条件 u(0,t) = u_0
    for i in range(1, len(u) - 1):
        u_tmp[i] = diff_eq_1d(u[(i - 1) : (i + 2)], D, dx, dt)
    u_tmp[-1] = 0  # 境界条件 u(x_e,t) = 0

    u = np.copy(u_tmp)
    t_list.append(t)
    u_list.append(np.copy(u))

# 01-01-03. 結果の可視化
import matplotlib.pyplot as plt

plt.figure(dpi=100)
plt.ylim(-0.05, 1.05)
for i in range(0, len(u_list), 100):
    plt.plot(x, u_list[i], ".-", label="t = " + str(t_list[i]))
    plt.legend(bbox_to_anchor=(1.05, 1), loc="upper left")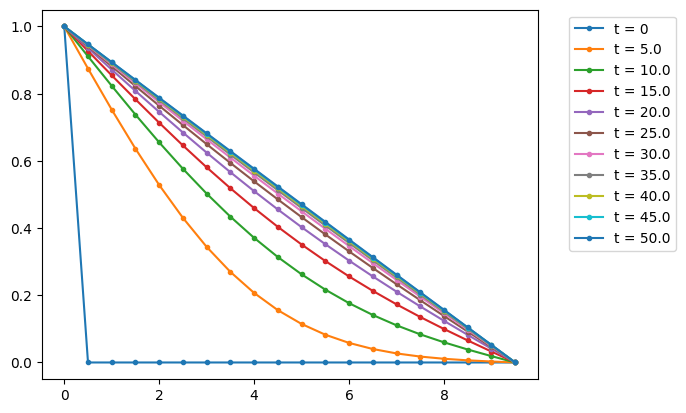

01-02. ２次元の拡散方程式¶

２次元の拡散方程式のプログラムを書く．周期境界条件でシミュレーションしてみよう． x軸方向，y軸方向とも空間方向の刻み幅１で，範囲はともに(-25,25)とする．初期条件はどこか１つの区画で100（ $u(x_s,y_s,0) = 100$ ）とする．

# 01-02-01. ２次元の拡散方程式の関数定義


def diff_eq_2d(u_arr, D, dh, dt):
    new_u = (
        u_arr[1, 1]
        + D
        * (
            (u_arr[0, 1] + u_arr[2, 1] + u_arr[1, 0] + u_arr[1, 2] - 4 * u_arr[1, 1])
            / (dh**2)
        )
        * dt
    )
    return new_u

# 01-02-02. ２次元の拡散方程式に基づく更新
def update(field, D, dh, dt):
    n_i, n_j = field.shape
    new_field = np.zeros((n_i, n_j), dtype=field.dtype)

    for i in range(n_i):
        for j in range(n_j):
            if i == 0:
                if j == 0:
                    # 境界条件処理 i=0,j=0
                    new_field[i, j] = diff_eq_2d(
                        field[[-1, 0, 1], :][:, [-1, 0, 1]], D, dh, dt
                    )
                elif 0 < j < n_j - 1:
                    # 境界条件処理 i=0,0<j<n_j-1
                    new_field[i, j] = diff_eq_2d(
                        field[[-1, 0, 1], :][:, [j - 1, j, j + 1]], D, dh, dt
                    )
                elif j == n_j - 1:
                    # 境界条件処理 i=0,j=n_j-1
                    new_field[i, j] = diff_eq_2d(
                        field[[-1, 0, 1], :][:, [n_j - 2, n_j - 1, 0]], D, dh, dt
                    )
            elif 0 < i < n_i - 1:
                if j == 0:
                    # 境界条件処理 1<i<n_i-1,j=0
                    new_field[i, j] = diff_eq_2d(
                        field[[i - 1, i, i + 1], :][:, [-1, 0, 1]], D, dh, dt
                    )
                elif 0 < j < n_j - 1:
                    # メイン （1<i<n_i-1,1<j<n_j-1）
                    new_field[i, j] = diff_eq_2d(
                        field[[i - 1, i, i + 1], :][:, [j - 1, j, j + 1]], D, dh, dt
                    )
                elif j == n_j - 1:
                    # 境界条件処理 1<i<n_i-1,j=n_j-1
                    new_field[i, j] = diff_eq_2d(
                        field[[i - 1, i, i + 1], :][:, [n_j - 2, n_j - 1, 0]], D, dh, dt
                    )
            elif i == n_i - 1:
                if j == 0:
                    # 境界条件処理 i=n_i,j=0
                    new_field[i, j] = diff_eq_2d(
                        field[[n_i - 2, n_i - 1, 0], :][:, [-1, 0, 1]], D, dh, dt
                    )
                elif 0 < j < n_j - 1:
                    # 境界条件処理 i=n_i-1,1<j<n_j-1
                    new_field[i, j] = diff_eq_2d(
                        field[[n_i - 2, n_i - 1, 0], :][:, [j - 1, j, j + 1]], D, dh, dt
                    )
                elif j == n_j - 1:
                    # 境界条件処理 i=n_i-1,j=n_j-1
                    new_field[i, j] = diff_eq_2d(
                        field[[n_i - 2, n_i - 1, 0], :][:, [n_j - 2, n_j - 1, 0]],
                        D,
                        dh,
                        dt,
                    )

    return new_field

# 01-02-p. ２次元の拡散方程式の擬似コード

各種パラメータ，初期値の設定
場の設定（x,y）

結果を記録するリストの定義

uの初期化

for ステップ数 in 繰り返し回数:
  時刻tの計算

  # -- 状態遷移 --
  u_tmp = update(u, D, dh, dt)

  情報の更新
  結果のリストへの記録

# 01-02-03. ２次元拡散モデルのシミュレーション実行
D = 1.0  # 拡散係数
dt = 0.05  # 時間方向の刻み幅
dh = 1  # 空間方向の刻み幅
u_0 = 100  # uの初期濃度

x = np.arange(-25, 25, dh)
y = np.arange(-25, 25, dh)
xmesh, ymesh = np.meshgrid(x, y)

t_end = 50  # tの終端

t_list = []  # 時刻を記録するリスト
u_list = []  # uを記録するリスト

u = np.zeros([len(x), len(y)], dtype=float)  # uの初期化
u[25, 25] = u_0  # 境界条件 u(0,t) = u_0

t_list.append(0)
u_list.append(np.copy(u))

for n in range(int(t_end / dt)):
    t = (n + 1) * dt  # 時刻tの計算

    # -- 状態遷移 --
    u_tmp = update(u, D, dh, dt)

    # 情報の更新
    t_list.append(t)
    u = np.copy(u_tmp)
    u_list.append(np.copy(u))

# 01-02-04a. 結果の可視化
fig, ax = plt.subplots(dpi=150)
ax.set_aspect("equal")
pcm = ax.pcolormesh(xmesh, ymesh, u_list[200], alpha=0.75, vmin=0, vmax=1)
fig.colorbar(pcm, ax=ax, shrink=0.8)
plt.show()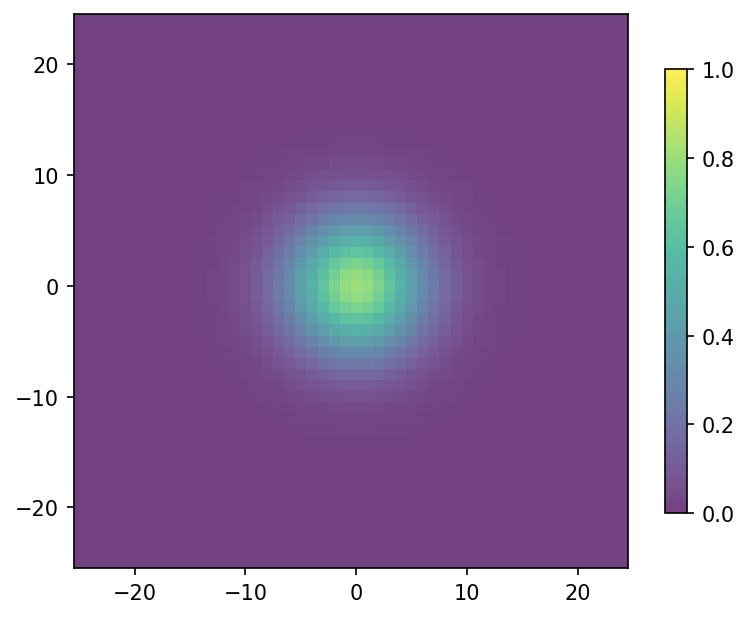

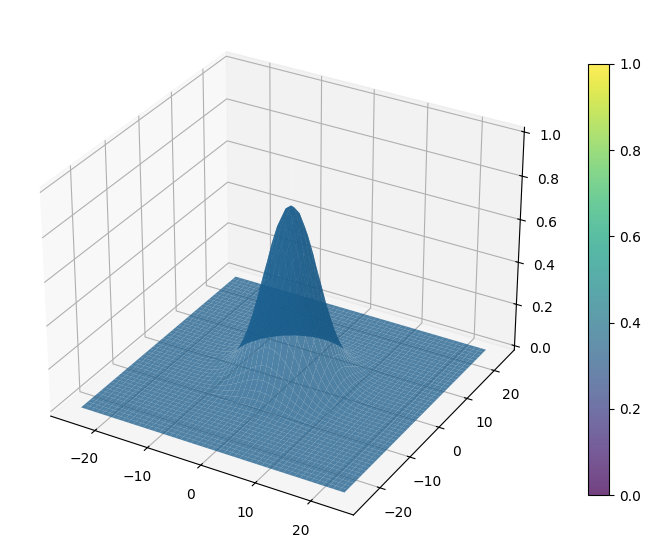
# 01-02-4b. 結果の可視化（3D）
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=(10, 7))
ax = fig.add_subplot(111, projection="3d")
surf = ax.plot_surface(xmesh, ymesh, u_list[200], vmin=0, vmax=1, alpha=0.75)
ax.plot([0, 0], [0, 0], [0, 1], "w", alpha=0.1)
fig.colorbar(surf, shrink=0.8)
plt.grid()
plt.show()