Skip to article frontmatterSkip to article content

11-03. ライフゲーム

03. ライフゲームのプログラムを組んでみてください．

03-01. ライフゲーム遷移ルール

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML

以下のような関数を定義してみよう．

def 遷移ルール(3x3の配列（注目するセルとその８近傍）):
    近傍の“生”（1）のセルの数を計算する（np.sumを使ってみよう）

    近傍の“生”のセルがちょうど２つならば:
        次世代の（中心の）セルの状態は更新なし
    （２ではなく）近傍の“生”のセルがちょうど3つならば:
        次世代の（中心の）セルの状態は“生”
    それ以外の場合（過疎，過密）:
        次世代の（中心の）セルの状態は“死”

    return 次世代の（中心の）セルの状態
Solution to Exercise 1
# 03-01. ライフゲーム遷移ルールの定義
def rule(cells):
    """Conway's Game of Lifeの遷移ルール

    入力された3x3の配列に基づき次世代の状態を返す．
    * 誕生：８近傍中ちょうど３つが1ならば次のステップで1
    * 維持：８近傍中ちょうど2つが1ならば次のステップで更新なし（1ならば1，0ならば0）
    * 過疎：８近傍中1が１つ以下ならば次のステップで0
    * 過密：８近傍中1が４つ以上ならば次のステップで0

    Args:
        cells: 3x3の配列．中心（cells[1,1]）とその８近傍．

    Returns:
        new_cell: 次世代の中心セルの状態．

    """

    num_neighbors = np.sum(cells) - cells[1, 1]
    if num_neighbors == 2:
        new_cell = np.copy(cells[1, 1])
    elif num_neighbors == 3:
        new_cell = 1
    else:
        new_cell = 0

    return new_cell

03-02. ライフゲームの実行

作成方針を以下に示す．

# 03-02. ライフゲームの実行
# 初期条件の設定
* 場のサイズを設定（縦，横にそれぞれ何個セルが配置されるか？）
* 何世代目まで計算するか？
* 場を記録するリストの準備
* 場の初期値の設定（例．ランダム，特定パタンの配置など）

for 世代:
    # 状態遷移
    次世代の場を記録する配列の用意

    for i in 場のサイズ（縦）:
        for j in 場のサイズ（横）:
            # 境界条件等による分岐
            # 全部で9通り（メイン+境界条件）
            もしi==0ならば:
                もしj==0ならば:
                    次世代の場[i,j] = 遷移ルール(場[[-1,0,1],:][:,[-1,0,1]])
                （j==0でなく）もし0<j<場のサイズ（横）-1ならば:
                    次世代の場[i,j] = 遷移ルール(場[[-1,0,1],:][:,[j-1,j,j+1]])
                （j<場のサイズ（横）-1でなく）もしj==場のサイズ（横）-1ならば:
                    …
            （i==0でなく）もし0<i<場のサイズ（縦）-1ならば:
                …
            （i<場のサイズ（縦）-1でなく）もしi==場のサイズ（縦）-1ならば:
                …

    場の更新（次世代を現世代にコピー, np.copyを使ってみよう）
    場の記録（リストへ追加）

場の更新をおこなう関数を定義してみよう．

Solution to Exercise 2
def update(field):
    """ライフゲームの更新

    `rule()`関数に従い，場の更新をおこなう．周期境界条件を仮定している．

    Args:
        field: 現在の場の配列
    Returns:
        new_field: 次世代の場の配列
    """
    n_i, n_j = field.shape
    new_field = np.zeros((n_i, n_j), dtype=field.dtype)

    for i in range(n_i):
        for j in range(n_j):
            if i == 0:
                if j == 0:
                    # 境界条件処理 i=0,j=0
                    new_field[i, j] = rule(field[[-1, 0, 1], :][:, [-1, 0, 1]])
                elif 0 < j < n_j - 1:
                    # 境界条件処理 i=0,0<j<n_j-1
                    new_field[i, j] = rule(field[[-1, 0, 1], :][:, [j - 1, j, j + 1]])
                elif j == n_j - 1:
                    # 境界条件処理 i=0,j=n_j-1
                    new_field[i, j] = rule(
                        field[[-1, 0, 1], :][:, [n_j - 2, n_j - 1, 0]]
                    )
            elif 0 < i < n_i - 1:
                if j == 0:
                    # 境界条件処理 1<i<n_i-1,j=0
                    new_field[i, j] = rule(field[[i - 1, i, i + 1], :][:, [-1, 0, 1]])
                elif 0 < j < n_j - 1:
                    # メイン （1<i<n_i-1,1<j<n_j-1）
                    new_field[i, j] = rule(
                        field[[i - 1, i, i + 1], :][:, [j - 1, j, j + 1]]
                    )
                elif j == n_j - 1:
                    # 境界条件処理 1<i<n_i-1,j=n_j-1
                    new_field[i, j] = rule(
                        field[[i - 1, i, i + 1],][:, [n_j - 2, n_j - 1, 0]]
                    )
            elif i == n_i - 1:
                if j == 0:
                    # 境界条件処理 i=n_i,j=0
                    new_field[i, j] = rule(field[[n_i - 2, n_i - 1, 0],][:, [-1, 0, 1]])
                elif 0 < j < n_j - 1:
                    # 境界条件処理 i=n_i-1,1<j<n_j-1
                    new_field[i, j] = rule(
                        field[[n_i - 2, n_i - 1, 0],][:, [j - 1, j, j + 1]]
                    )
                elif j == n_j - 1:
                    # 境界条件処理 i=n_i-1,j=n_j-1
                    new_field[i, j] = rule(
                        field[[n_i - 2, n_i - 1, 0],][:, [n_j - 2, n_j - 1, 0]]
                    )

    return new_field

定義したupdateを使ってシミュレーションをしてみよう．

以下では例としてグライダー銃のパターンを使ってシミュレーションする．

# グライダー銃
ptn_glidergun = np.array([
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1],
    [1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
], dtype=int)
# 03-02. ライフゲームの実行
n_i = 50
n_j = 50
steps = 50

field_list = []
field = np.zeros((n_i,n_j),dtype=int)


field[5:5+ptn_glidergun.shape[0],5:5+ptn_glidergun.shape[1]] = np.copy(ptn_glidergun)
# field=np.random.randint(2,size=field_size,dtype=int)

field_list.append(field)
for t in range(1,steps+1):
    if t%10 == 0:
        print("Steps: ", t)
    # -- 状態遷移 --
    field_tmp = update(field)

    # 情報の更新
    field = np.copy(field_tmp)
    field_list.append(field)
Steps:  10

Steps:  20

Steps:  30

Steps:  40

Steps:  50

03-03. セルオートマトンの可視化

# 03-03. セルオートマトンの可視化
plt.figure(figsize=(8, 8))
plt.matshow(field_list[50], fignum=1, cmap="binary")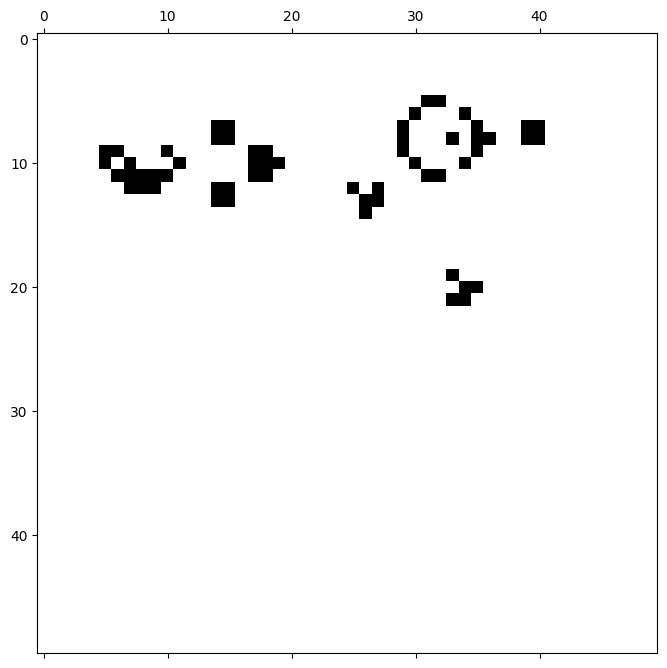
<Figure size 800x800 with 1 Axes>

03-04. セルオートマトンの可視化 アニメーション

# 03-04. セルオートマトンの可視化 アニメーション
from matplotlib import animation, rc
from IPython.display import HTML

fig, ax = plt.subplots(dpi=150)
plt.close()

artists = []

for i in range(len(field_list)):
    im = ax.matshow(field_list[i], interpolation="none", cmap="binary")

    ax.set_aspect("equal")
    artists.append([im])

# アニメーションへの変換
ani = animation.ArtistAnimation(fig, artists, interval=100)

# アニメーションの表示（JavaScriptとして埋め込み）
rc("animation", html="jshtml")
ani
Loading...

ライフゲームのパターンの例

LifeWikiにて，多数のパターンを見つけることができる．

また，パターンをテキストしてコピーしたり，ファイルとしてダウンロードできる．

以下にはいくつかの例を示す．

グライダー

# グライダー
ptn_glider = np.array([[1, 1, 1], [1, 0, 0], [0, 1, 0]], dtype=int)

回転花火

# 回転花火
ptn_pinwheel = np.array(
    [
        [0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0],
        [1, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0],
        [1, 1, 0, 1, 0, 0, 1, 0, 1, 0, 0, 0],
        [0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1],
        [0, 0, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1],
        [0, 0, 0, 0, 1, 1, 1, 1, 0, 0, 0, 0],
        [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0],
        [0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0],
    ],
    dtype=int,
)

グライダー銃

# グライダー銃
ptn_glidergun = np.array([
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1],
    [1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
], dtype=int)

パン屋

# パン屋
ptn_baker = np.array([
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
], dtype=int)
応用編
11-02. セルオートマトン
応用編
12 パターン形成，反応拡散モデル