06-02 ランダムウォーク，ライト-フィッシャー モデル
待ち時間，ランダムウォーク¶
02-01. サイコロの目の総和が100を超えるまでの待ち時間¶
# 02-01. サイコロの目の総和が100を超えるまでの待ち時間
import randomx = 0
for i in range(100):
r = random.randrange(1, 7)
x = x + r
print(str(i + 1) + "回目：", x)
if x >= 100:
print(str(i + 1) + "回目で100を超えた．")
break1回目： 4
2回目： 10
3回目： 12
4回目： 18
5回目： 19
6回目： 23
7回目： 26
8回目： 28
9回目： 32
10回目： 35
11回目： 36
12回目： 39
13回目： 44
14回目： 48
15回目： 54
16回目： 57
17回目： 60
18回目： 65
19回目： 68
20回目： 70
21回目： 73
22回目： 76
23回目： 82
24回目： 88
25回目： 89
26回目： 90
27回目： 93
28回目： 95
29回目： 100
29回目で100を超えた．
02-02a. ランダムウォーク choice¶
# 02-02a. ランダムウォーク choice
x = 0
x_list = [x]
for i in range(100):
r = random.choice([-1, 1])
x = x + r
x_list.append(x)import matplotlib.pyplot as pltplt.plot(x_list)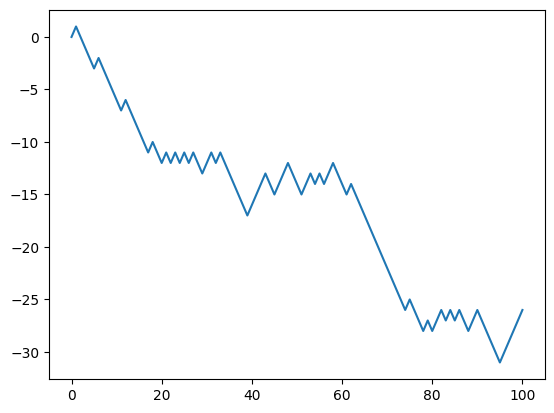
02-02b ランダムウォーク randrange¶
# 02-02b ランダムウォーク randrange
x = 0
x_list = [x]
for i in range(100):
r = random.randrange(-1, 2, 2)
x = x + r
x_list.append(x)plt.plot(x_list)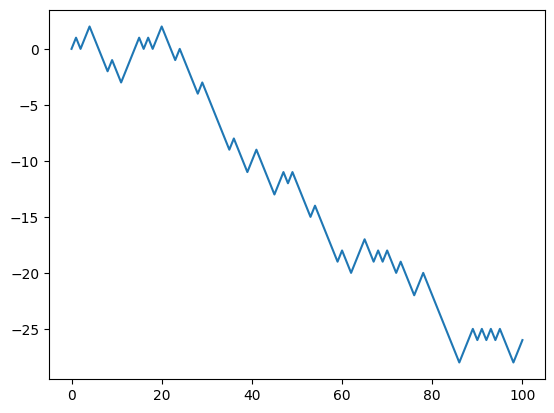
02-03. ランダムウォークの待ち時間¶
# 02-03. ランダムウォークの待ち時間
x = 0
x_list = [x]
for i in range(10000):
r = random.choice([-1, 1])
x = x + r
x_list.append(x)
if x >= 10:
break
print("待ち時間：", len(x_list) - 1)待ち時間： 48
plt.plot(x_list)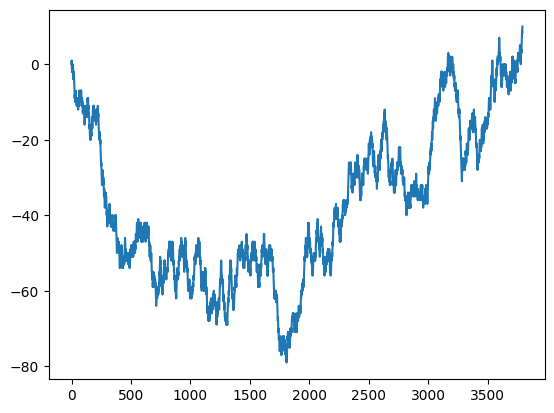
ライトフィッシャー モデル¶
02-04. ライト-フィッシャー モデル¶
# 02-04. ライト-フィッシャー モデル
pop_size = 100
gen_end = 200
# aの初期値の設定
a = []
for i in range(pop_size):
if i % 2 == 0:
a.append(0)
else:
a.append(1)
a_list = [a.copy()]
for t in range(gen_end):
# a_newの初期化
a_new = []
for i in range(pop_size):
p1 = random.randrange(pop_size)
p2 = random.randrange(pop_size)
r = random.choice([a[p1], a[p2]])
a_new.append(r)
a = a_new.copy()
a_list.append(a.copy())# 結果の表示
for a in a_list:
print(a)Fetching long content....
02-05. matshowによる可視化¶
# 02-05. matshowによる可視化
plt.matshow(a_list, interpolation=None, vmin=0, vmax=1)
plt.ylabel("generation")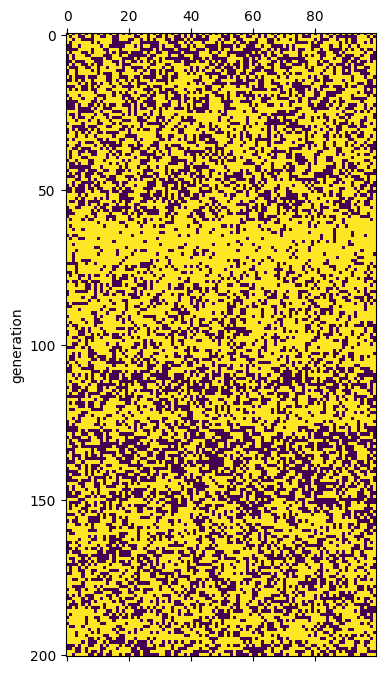
02-06. 頻度の世代を経た変化¶
# 02-06. 頻度の世代を経た変化
p_list = []
q_list = []
for a in a_list:
p = sum(a) / len(a)
p_list.append(p)
q_list.append(1 - p)plt.plot(p_list, "-", q_list, "-")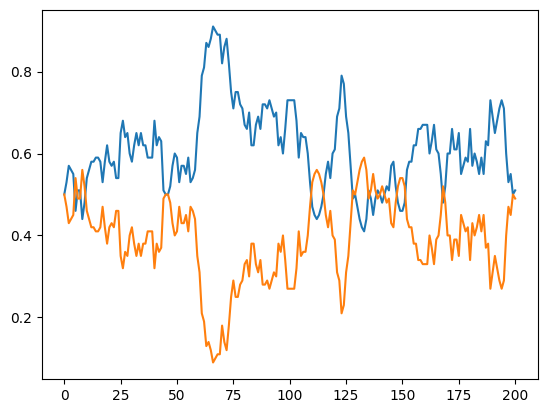
リストのコピー¶
問題にならないケース¶
# 問題にならないケース
a_list = []
for i in range(10):
a = [i, i, i]
a_list.append(a)
print(a_list)[[0, 0, 0], [1, 1, 1], [2, 2, 2], [3, 3, 3], [4, 4, 4], [5, 5, 5], [6, 6, 6], [7, 7, 7], [8, 8, 8], [9, 9, 9]]
問題になるケース¶
# 問題になるケース
a_list = []
a = [0, 0, 0]
for i in range(10):
for j in range(3):
a[j] = i
a_list.append(a)
print(a_list)[[9, 9, 9], [9, 9, 9], [9, 9, 9], [9, 9, 9], [9, 9, 9], [9, 9, 9], [9, 9, 9], [9, 9, 9], [9, 9, 9], [9, 9, 9]]
修正¶
# 修正
a_list = []
a = [0, 0, 0]
for i in range(10):
for j in range(3):
a[j] = i
a_list.append(a.copy())
print(a_list)[[0, 0, 0], [1, 1, 1], [2, 2, 2], [3, 3, 3], [4, 4, 4], [5, 5, 5], [6, 6, 6], [7, 7, 7], [8, 8, 8], [9, 9, 9]]
突然変異固定までの待ち時間¶
02-07. 突然変異固定までの平均待ち時間を10回分について計算してみよう¶
Solution to Exercise 1
例は以下の通り．
# 待ち時間
num_trials = 10
pop_size = 100
init_num_target = int(pop_size / 2)
waiting_time = []
for n in range(1000):
a = []
for i in range(pop_size):
if i < init_num_target:
a.append(0)
else:
a.append(1)
a_list = [a.copy()]
for t in range(100000):
a_new = []
for i in range(pop_size):
p1 = random.randrange(pop_size)
p2 = random.randrange(pop_size)
r = random.choice([a[p1], a[p2]])
a_new.append(r)
a = a_new.copy()
a_list.append(a.copy())
if (sum(a) == 0 or sum(a) == pop_size):
break
if sum(a_list[-1]) == 0 or sum(a_list[-1]) == pop_size:
waiting_time.append(len(a_list))
if len(waiting_time) >= num_trials:
break# 平均待ち時間
sum(waiting_time) / len(waiting_time)148.2関数を使うと，見通しが良くなる． 別の例は以下の通り．
def wright_fisher_Model(pop_size, gen_end, init_num_target, extinct_break=False):
"""Wright-Fisher model
ハプロタイプを仮定したライト-フィッシャーモデルに基づく遺伝的浮動．
Args:
pop_size: 集団サイズ
gen_end: 最終世代
init_num_target: 注目している遺伝子型の初期数
extinct_break: どちらかの遺伝子型が絶滅した場合に処理を中断するか
Returns:
a_list: 各世代の遺伝子型を記録したリスト
"""
if pop_size < init_num_target:
print(
"注目する遺伝子型の初期値`init_num_target`は集団サイズ`pop_size`以下でなければならない．"
)
return
a = []
for i in range(pop_size):
if i < init_num_target:
a.append(0)
else:
a.append(1)
a_list = [a.copy()]
for t in range(gen_end):
a_new = []
for i in range(pop_size):
p1 = random.randrange(pop_size)
p2 = random.randrange(pop_size)
r = random.choice([a[p1], a[p2]])
a_new.append(r)
a = a_new.copy()
a_list.append(a.copy())
if ((sum(a) == pop_size) or (sum(a) == 0)) and extinct_break:
break
return a_list# 待ち時間
num_trials = 10
pop_size = 100
init_num_target = int(pop_size / 2)
waiting_time = []
for n in range(1000):
a_list = wright_fisher_Model(pop_size, 100000, init_num_target, extinct_break=True)
if sum(a_list[-1]) == 0 or sum(a_list[-1]) == pop_size:
waiting_time.append(len(a_list))
if len(waiting_time) >= num_trials:
break# 平均待ち時間
sum(waiting_time) / len(waiting_time)149.0